Giải toán 8 tập 2 trang 77 Bài 4: Hai hình đồng dạng
Giải toán 8 tập 2 trang 77 Bài 4: Hai hình đồng dạng
Giải toán 8 tập 2 trang 77 bài 4 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 8 tập 2 trang 77
Giải Hoạt động 1 trang 77 toán 8 tập 2
a) Cho đoạn thẳng $AB$ và điểm $O$. Kẻ các tia $OA,OB$. Trên tia $OA,OB$ lần lượt lấy các điểm $A’,B’$ sao cho $OA’ = 3OA,OB’ = 3OB$ (hình 1a).
i) $A’B’$ có song song với $AB$ không.
ii) Tính tỉ số $\frac{{A’B’}}{{AB}}$.
b) Cho tam giác $ABC$ và điểm $O$. Kẻ các tia $OA,OB,OC$. Trên tia $OA,OB,OC$ lần lượt lấy các điểm $A’,B’,C’$ sao cho $OA’ = 3OA,OB’ = 3OB,OC’ = 3OC$ (Hình 1b).
i) Tính và so sánh các tỉ số $\frac{{A’B’}}{{AB}},\frac{{A’C’}}{{AC}},\frac{{B’C’}}{{BC}}$.
ii) Chứng minh tam giác $A’B’C’$ đồng dạng với tam giác $ABC$.

Hướng dẫn giải
a)
i) Vì $OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}$;$OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}$.
Xét tam giác $OA’B’$ có:
$\frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{1}{3}$
Do đó, $A’B’//AB$ (định lí Thales đảo)
ii) Vì $A’B’//AB \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{{AB}}{{A’B’}} = \frac{1}{3}$ (hệ quả của định lí Thales)
Do đó, $\frac{{A’B’}}{{AB}} = \frac{3}{1} = 3$.
b)
i)
– Vì $OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}$;$OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}$.
Xét tam giác $OA’B’$ có:
$\frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{1}{3}$
Do đó, $A’B’//AB$ (định lí Thales đảo)
Vì $A’B’//AB \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OB}}{{OB’}} = \frac{{AB}}{{A’B’}} = \frac{1}{3}$ (hệ quả của định lí Thales)
Do đó, $\frac{{A’B’}}{{AB}} = \frac{3}{1} = 3$.
– Vì $OA’ = 3OA \Rightarrow \frac{{OA}}{{OA’}} = \frac{1}{3}$;$OC’ = 3OC \Rightarrow \frac{{OC}}{{OC’}} = \frac{1}{3}$.
Xét tam giác $OA’C’$ có:
$\frac{{OA}}{{OA’}} = \frac{{OC}}{{OC’}} = \frac{1}{3}$
Do đó, $A’C’//AC$ (định lí Thales đảo)
Vì $A’C’//AC \Rightarrow \frac{{OA}}{{OA’}} = \frac{{OC}}{{OC’}} = \frac{{AC}}{{A’C’}} = \frac{1}{3}$ (hệ quả của định lí Thales)
Do đó, $\frac{{A’C’}}{{AC}} = \frac{3}{1} = 3$.
– Vì $OB’ = 3OB \Rightarrow \frac{{OB}}{{OB’}} = \frac{1}{3}$;$OC’ = 3OC \Rightarrow \frac{{OC}}{{OC’}} = \frac{1}{3}$.
Xét tam giác $OB’C’$ có:
$\frac{{OB}}{{OB’}} = \frac{{OC}}{{OC’}} = \frac{1}{3}$
Do đó, $B’C’//BC$ (định lí Thales đảo)
Vì $B’C’//BC \Rightarrow \frac{{OB}}{{OB’}} = \frac{{OC}}{{OC’}} = \frac{{BC}}{{B’C’}} = \frac{1}{3}$ (hệ quả của định lí Thales)
Do đó, $\frac{{B’C’}}{{BC}} = \frac{3}{1} = 3$.
Do đó, $\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}$
ii) Xét tam giác $A’B’C’$ và tam giác $ABC$ ta có:
$\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}$ (chứng minh trên)
Do đó, tam giác $A’B’C’$ đồng dạng với tam giác $ABC$.
Giải Hoạt động 2 trang 77 toán 8 tập 2
Cho tứ giác ABCD và điểm O(O không thuộc các đường thẳng AB, BC, CD, DA). Trên các tia $OA,OB,OC,OD$ lần lượt lấy các điểm $A’,B’,C’,D’$ sao cho $OA’ = \frac {1}{2} OA,OB’ = \frac {1}{2} OB,OC’ = \frac {1}{2} OC,OD’ = \frac {1}{2} OD$ (Hình 2).
Tính và so sánh các tỉ số $\frac{{A’B’}}{{AB}};\frac{{A’D’}}{{AD}};\frac{{B’C’}}{{BC}};\frac{{C’D’}}{{CD}}$.

Hướng dẫn giải
– Vì $OA’ = \frac {1}{2} OA \Rightarrow \frac{{OA’}}{{OA}} = \frac{1}{2}$;$OB’ = \frac {1}{2} OB \Rightarrow \frac{{OB’}}{{OB}} = \frac{1}{2}$.
Xét tam giác $OAB$ có:
$\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}} = \frac{1}{2}$
Do đó, $A’B’//AB$ (định lí Thales đảo)
Vì $A’B’//AB \Rightarrow \frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}} = \frac{{A’B’}}{{AB}} = \frac{1}{2}$ (hệ quả của định lí Thales)
– Vì $OA’ = \frac {1}{2} OA \Rightarrow \frac{{OA’}}{{OA}} = \frac{1}{2}$;$OD’ = \frac {1}{2}OD \Rightarrow \frac{{OD’}}{{OD}} = \frac{1}{2}$.
Xét tam giác $OAD$ có:
$\frac{{OA’}}{{OA}} = \frac{{OD’}}{{OD}} = \frac{1}{2}$
Do đó, $A’D’//AD$ (định lí Thales đảo)
Vì $A’D’//AD \Rightarrow \frac{{OA’}}{{OA}} = \frac{{OD’}}{{OD}} = \frac{{A’D’}}{{AD}} = \frac{1}{2}$ (hệ quả của định lí Thales)
– Vì $OB’ = \frac {1}{2} OB \Rightarrow \frac{{OB’}}{{OB}} = \frac{1}{2}$;$OC’ = \frac {1}{2} OC \Rightarrow \frac{{OC’}}{{OC}} = \frac{1}{2}$.
Xét tam giác $OBC$ có:
$\frac{{OB’}}{{OB}} = \frac{{OC’}}{{OC}} = \frac{1}{2}$
Do đó, $B’C’//BC$ (định lí Thales đảo)
Vì $B’C’//BC \Rightarrow \frac{{OB’}}{{OB}} = \frac{{OC’}}{{OC}} = \frac{{B’C’}}{{BC}} = \frac{1}{2}$ (hệ quả của định lí Thales)
– Vì $OD’ = \frac {1}{2} OD \Rightarrow \frac{{OD’}}{{OD}} = \frac{1}{2}$;$OC’ = \frac {1}{2}OC \Rightarrow \frac{{OC’}}{{OC}} = \frac{1}{2}$.
Xét tam giác $ODC$ có:
$\frac{{OD’}}{{OD}} = \frac{{OC’}}{{OC}} = \frac{1}{2}$
Do đó, $D’C’//DC$ (định lí Thales đảo)
Vì $D’C’//DC \Rightarrow \frac{{OD’}}{{OD}} = \frac{{OC’}}{{OC}} = \frac{{D’C’}}{{DC}} = \frac{1}{2}$ (hệ quả của định lí Thales)
Do đó, $\frac{{B’C’}}{{BC}} = \frac{{A’B’}}{{AB}} = \frac{{C’D’}}{{CD}} = \frac{{A’D’}}{{AD}}$.
Giải toán 8 tập 2 trang 78
Thực hành 1 trang 78 toán 8 tập 2
Cho ba tấm ảnh được đặt trên lưới ô vuông như Hình 4. Hãy chỉ ra ba cặp hình, trong mỗi cặp hình này đồng dạng phối cảnh với hình kia và chỉ ra tỉ số đồng dạng tương ứng.

Hướng dẫn giải
Ta tiến hành đo và nhận thấy hình $ABCD$ là hình đồng dạng phối cảnh với hình $A’B’C’D’$ theo tỉ số $k = \frac {AB}{A’B’} = \frac {BC}{B’C’} = \frac {8}{4} = \frac {6}{3} = 2$.
Ta tiến hành đo và nhận thấy hình $A’B’C’D’$ là hình đồng dạng phối cảnh với hình $A”B”C”D”$ theo tỉ số $k = \frac {A’B’}{A”B”} = \frac {B’C’}{B”C”} = \frac {4}{12} = \frac {3}{9} = \frac {1}{3}$.
=> Hình $ABCD$ đồng dạng phối cảnh với hình $A”B”C”D”$ theo tỉ số $k = 2.\frac {1}{3} = \frac {2}{3}$
Giải toán 8 tập 2 trang 79
Hoạt động 3 trang 79 toán 8 tập 2
Trong hình 5, biết $H_1$ đồng dạng phối cảnh với hình H tỉ số $k = \frac{3}{2}$.
a) Tính $x,y$.
b) So sánh hình ${H_1}$ và hình $H’$.

Hướng dẫn giải
a) Vì hai hình đồng dạng phối cảnh $H$ và ${H_1}$ có tỉ số đồng dạng $k = \frac{2}{3}$ nên $\frac{{3,6}}{x} = \frac{2}{y} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}\frac{{3,6}}{x} = \frac{2}{3}\\\frac{2}{y} = \frac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 5,4\\y = 3\end{array} \right.$
Vậy $x = 5,4cm;y = 3cm$.
b) Hình ${H_1}$ và hình $H’$ là hai hình bằng nhau vì chúng có kích thước bằng nhau và khi ta đặt hình ${H_1}$ nằm ngang sẽ thu được hình $H’$.
Thực hành 2 trang 79 toán 8 tập 2
Trong hình 7 dưới đây, hãy chọn ra các cặp hình đồng dạng với nhau. Tìm tỉ số đồng dạng tương ứng.
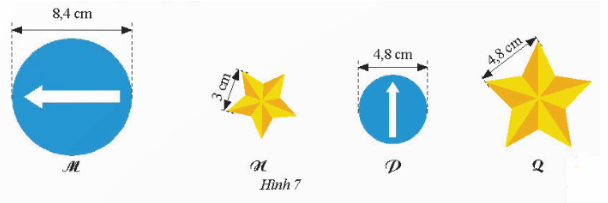
Hướng dẫn giải
Hình M và P đồng dạng theo tỉ số $k = \frac {8,4}{4,8} = \frac {7}{4}$
Hình N và Q đồng dạng theo tỉ số $k = \frac {3}{4,8} = \frac {5}{8}$
Giải toán 8 tập 2 trang 80
Vận dụng trang 80 toán 8 tập 2
Trong Hình 8b, c, d, Hình nào đồng dạng với Hình 8a. Giải thích.
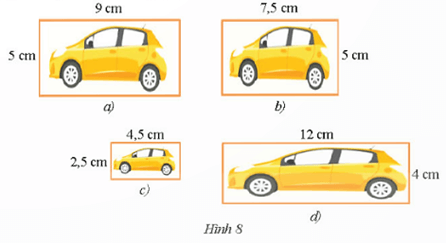
Hướng dẫn giải
– Xét hình 8a và hình 8b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8b lần lượt là:
$\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
– Xét hình 8a và hình 8c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8c lần lượt là:
$\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2$. Do đó, tồn tại hình động dạng phối cảnh của hình 8a bằng hình 8c (hình 8a thu nhỏ với tỉ số 2). Do đó, hình 8a và hình 8c đồng dạng với nhau.
– Xét hình 8a và hình 8d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8d lần lượt là:
$\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
Bài tập
Giải toán 8 tập 2 trang 82
Bài 1 trang 82 Toán 8 Tập 2:
Trong các hình dưới đây, hãy chọn ra các cặp hình đồng dạng.

Hướng dẫn giải
Quan sát Hình 14, ta thấy:
Các cặp hình đồng dạng: Hình 14a và Hình 14g; Hình d và Hình d; Hình c và Hình e.
Bài 2 trang 82 Toán 8 Tập 2:
Trong các hình dưới đây, hai hình nào đồng dạng với nhau?

Hướng dẫn giải
– Xét hình 16a và hình 16b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16b lần lượt là:
$\frac{3}{{4,5}} = \frac{2}{3};\frac{{2,6}}{{3,9}} = \frac{2}{3}$. Do đó, tồn tại hình động dạng phối cảnh của hình 16a bằng hình 16b. Do đó, hình 16a và hình 16b đồng dạng với nhau.
– Xét hình 16b và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16b và hình 16c lần lượt là:
$\frac{{4,5}}{3} = 1,5;\frac{{3,9}}{2} = 1,95$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16b để bằng hình 16c. Do đó, hình 16b và hình 16c không đồng dạng với nhau.
– Xét hình 16c và hình 16c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 16a và hình 16c lần lượt là:
$\frac{3}{3} = 1;\frac{{2,6}}{2} = 1,3$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 16a để bằng hình 16c. Do đó, hình 16a và hình 16c không đồng dạng với nhau.
Giải toán 8 tập 2 trang 83
Bài 3 trang 83 Toán 8 Tập 2:
Trong các Hình 17b, c, d hình nào đồng dạng với Hình 17a? Giải thích?
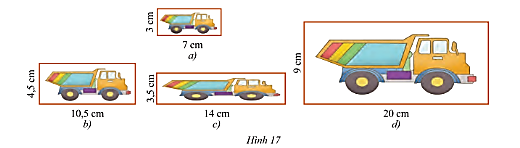
Hướng dẫn giải
– Xét hình 17a và hình 17b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17b lần lượt là:
$\frac{7}{{10,5}} = \frac{2}{3};\frac{3}{{4,5}} = \frac{2}{3}$. Do đó, tồn tại hình động dạng phối cảnh của hình 17a bằng hình 17b. Do đó, hình 17a và hình 17b đồng dạng với nhau.
– Xét hình 17a và hình 17c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17c lần lượt là:
$\frac{7}{{14}} = \frac{1}{2};\frac{3}{{3,5}} = \frac{6}{7}$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 17a để bằng hình 17c. Do đó, hình 17a và hình 17c không đồng dạng với nhau.
– Xét hình 17a và hình 17d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 17a và hình 17d lần lượt là:
$\frac{7}{{20}};\frac{3}{9} = \frac{1}{3}$. Do đó, không tồn tại hình động dạng phối cảnh nào của hình 17a để bằng hình 17d. Do đó, hình 17a và hình 17d không đồng dạng với nhau.
Bài 4 trang 83 Toán 8 Tập 2:
Hình 18b là Hình 18a sau khi phóng to với $k = 1,5$. Nếu kích thức của Hình 18a là $4 \times 6$thì kích thước của Hình 18b là bao nhiêu?

Hướng dẫn giải
Vì hình 18b là Hình 18a sau khi phóng to với $k = 1,5$ nên kích thước Hình 18b sẽ gấp 1,5 lần kích thước Hình 18a.
Ta có: $4.1,5 = 6;6.1,5 = 9$.
Do đó, kích thước của hình 18b là $6 \times 9$.
