Giải toán 8 tập 2 trang 21 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Giải toán 8 tập 2 trang 21 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Giải toán 8 tập 2 trang 21 bài 3 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 8 tập 2 trang 16
Khởi động trang 16 toán 8 tập 2
Có một cái bể đã chứa sẵn 5 ${m^3}$ nước. Người ta bắt đầu mở một vòi nước cho chảy vào bể, mỗi giờ chảy được 2 ${m^3}$. Hãy tính:
a) Lượng nước chảy vào bể sau 1 giờ.
b) Lượng nước chảy vào bể sau $x$ giờ.
c) Lượng nước $y$ có trong bể sau $x$ giờ.
Hướng dẫn giải
a) Lượng nước chảy vào bể sau 1 giờ là:
$1.2 = 2\left( {{m^3}} \right)$
b) Lượng nước chảy vào bể sau $x$ giờ là:
$2.x = 2x\left( {{m^3}} \right)$
c) Lượng nước ban đầu của bể là $ 5\left( {{m^3}} \right)$.
Lượng nước $y$ có trong bể sau $x$ giờ là:
$y = 2x + 5\left( {{m^3}} \right)$.
HĐ1 trang 16 toán 8 tập 2
Trong thực tế chúng ta thường gặp các mô hình dẫn đến những hàm số có dạng như: $y = 2x + 5;y = – x + 4;y = 5x…$
Những hàm số này được gọi là hàm số bậc nhất. Vậy hàm số bậc nhất có dạng như thế nào?
Hướng dẫn giải:
Ta thấy tất cả các hàm số đã cho đều có dạng $y = ax + b$
$y = 2x + 5$ với $a = 2;b = 5$; $y = – x + 4$ với $a = – 1;b = 4$; $y = 5x$ với $a = 5;b = 0$
Do đó, hàm số bậc nhất là hàm số được cho bởi công thức $y = ax + b$ với $a,b$ là các số cho trước và $a \ne 0$.
THựC HÀNH 1 trang 16 toán 8 tập 2
Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số $a,b$ của các hàm số đó:
$y = 4x – 7$;$y = {x^2}$;$y = – 6x – 4$;$y = 4x$;$y = \dfrac{3}{x}$;$s = 5v + 8$;$m = 30n – 25$.
Hướng dẫn giải:
– Hàm số$y = 4x – 7$ là hàm số bậc nhất vì hàm số có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 4;b = – 7$.
– Hàm số $y = {x^2}$ không là hàm số bậc nhất vì hàm số không có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$.
– Hàm số $y = – 6x – 4$là hàm số bậc nhất vì hàm số có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = – 6;b = – 4$.
– Hàm số $y = 4x$là hàm số bậc nhất vì hàm số có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 4;b = 0$.
– Hàm số $y = \dfrac{3}{x}$ không là hàm số bậc nhất vì hàm số không có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$.
– Hàm số $s = 5v + 8$ là hàm số bậc nhất vì hàm số có dạng $s = av + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 5;b = 8$.
– Hàm số $m = 30n – 25$ là hàm số bậc nhất vì hàm số có dạng $m = an + b$với $a,b$ là các số cho trước và $a \ne 0$. Hệ số $a = 30;b = – 25$.
VậN DụNG 1 trang 16 toán 8 tập 2
Một hình chữ nhật có các kích thước là $2m$ và $3m$. Gọi $y$ là chu vi của hình chữ nhật này sau khi tăng chiều dài và chiều rộng thêm $x\left( m \right)$. Hãy chứng tỏ $y$là một hàm số bậc nhất theo biến số $x$. Tìm các hệ số $a;b$ của hàm số này.
Hướng dẫn giải:
Sau khi tăng chiều dài thêm $x\left( m \right)$ thì chiều dài mới của hình chữ nhật là $3 + x\left( m \right)$
Sau khi tăng chiều rộng thêm $x\left( m \right)$ thì chiều rộng mới của hình chữ nhật là $2 + x\left( m \right)$
Chu vi mới của hình chữ nhật là:
$y = \left( {3 + x + 2 + x} \right).2$
$ \Leftrightarrow y = \left( {5 + 2x} \right).2$
$ \Leftrightarrow y = 4x + 10$
Vì hàm số $y = 4x + 10$ có dạng $y = ax + b$với $a,b$ là các số cho trước và $a \ne 0$.
Nên hàm số $y = 4x + 10$ là hàm số bậc nhất.
Do đó $y$ là một hàm số bậc nhất theo biến số $x$, hệ số $a = 4;b = 10$.
Giải toán 8 tập 2 trang 17
HOạT ĐộNG 2 trang 17 toán 8 tập 2
Lượng nước $y$ (tính theo ${m^3}$) có trong một bể nước sau $x$ giờ mở vòi cấp nước được cho bởi hàm số $y = 2x + 3$. Tính lượng nước có trong bể sau 0 giờ; 1 giờ; 2 giờ; 3 giờ; 10 giờ và hoàn thành bảng giá trị sau:

Hướng dẫn giải:
+ Với $x = 0$ giờ $ \Rightarrow y = 2.0 + 3 = 3\left( {{m^3}} \right)$;
+ Với $x = 1$ giờ $ \Rightarrow y = 2.1 + 3 = 5\left( {{m^3}} \right)$;
+ Với $x = 2$ giờ $ \Rightarrow y = 2.2 + 3 = 7\left( {{m^3}} \right)$;
+ Với $x = 3$ giờ $ \Rightarrow y = 2.3 + 3 = 9\left( {{m^3}} \right)$;
+ Với $x = 10$ giờ $ \Rightarrow y = 2.10 + 3 = 23\left( {{m^3}} \right)$.
Ta có bảng sau
| $x$ | 0 | 1 | 2 | 3 | 10 |
| $y = f\left( x \right) = 2x + 3$ | 3 | 5 | 7 | 9 | 23 |
THựC HÀNH 2 trang 17 toán 8 tập 2
Lập bảng giá trị của mỗi hàm số bậc nhất sau:
$y = f\left( x \right) = 4x – 1$ và $y = h\left( x \right) = – 0,5x + 8$ với $x$ lần lượt bằng –3; –2; –1; 0; 1; 2; 3.
Hướng dẫn giải:
+ Với $x = – 3$$ \Rightarrow f\left( { – 3} \right) = 4.\left( { – 3} \right) – 1 = – 13;g\left( { – 3} \right) = – 0,5.\left( { – 3} \right) + 8 = 9,5$;
+ Với $x = – 2$$ \Rightarrow f\left( { – 2} \right) = 4.\left( { – 2} \right) – 1 = – 9;g\left( { – 2} \right) = – 0,5.\left( { – 2} \right) + 8 = 9$;
+ Với $x = – 1$$ \Rightarrow f\left( { – 1} \right) = 4.\left( { – 1} \right) – 1 = – 5;g\left( { – 1} \right) = – 0,5.\left( { – 1} \right) + 8 = 8,5$;
+ Với $x = 0$$ \Rightarrow f\left( 0 \right) = 4.0 – 1 = – 1;g\left( 0 \right) = – 0,5.0 + 8 = 8$;
+ Với $x = 1$$ \Rightarrow f\left( 1 \right) = 4.1 – 1 = 3;g\left( 1 \right) = – 0,5.1 + 8 = 7,5$;
+ Với $x = 2$$ \Rightarrow f\left( 2 \right) = 4.2 – 1 = 7;g\left( 2 \right) = – 0,5.2 + 8 = 7$;
+ Với $x = 3$$ \Rightarrow f\left( 3 \right) = 4.3 – 1 = 11;g\left( 3 \right) = – 0,5.3 + 8 = 6,5$.
Ta có bảng sau:
| $x$ | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| $y = f\left( x \right) = 4x – 1$ | –13 | –9 | –5 | –1 | 3 | 7 | 11 |
| $y = g\left( x \right) = – 0,5x + 8$ | 9,5 | 9 | 8,5 | 8 | 7,5 | 7 | 6,5 |
Vận dụng 2 trang 17 toán 8 tập 2
Một xe khách khởi hành từ bến xe phía Bắc bưu điện thành phố Nha Trang để đi ra thành phố Đà Nẵng với tốc độ 40 km/h (Hình 2).

a) Biết rằng bến xe cách bưu điện thành phố Nha Trang 6 km. Sau $x$ giờ, xe khách cách bưu điện thành phố Nha Trang $y$km. Tính $y$ theo $x$.
b) Chứng minh rằng $y$ là một hàm số bậc nhất theo biến $x$.
c) Hoàn thành bảng giá trị của hàm số ở câu b) và giải thích ý nghĩa của bảng giá trị này:

Hướng dẫn giải:
a) Quãng đường xe khách đi được sau x giờ với vận tốc 40 km/h là $40.x$ (km)
Vì ban đầu bến xe cách bưu điện Nha Trang 6 km nên sau x giờ xe khách cách bưu điện thành phố Nha Trang số km là: $40x + 6$. Do đó, $y = 40x + 6$ với $y$ là số km xe khách cách bưu điện thành phố Nha Trang sau $x$ giờ.
b) Vì hàm số $y = 40x + 6$ có dạng $y = ax + b$ với $a = 40;b = 6$ nên $y$ là một hàm số bậc nhất theo biến $x$.
c)
– Với $x = 0 \Rightarrow y = f\left( 0 \right) = 40.0 + 6 = 6$;
– Với $x = 1 \Rightarrow y = f\left( 1 \right) = 40.1 + 6 = 46$;
– Với $x = 2 \Rightarrow y = f\left( 2 \right) = 40.2 + 6 = 86$;
– Với $x = 3 \Rightarrow y = f\left( 3 \right) = 40.3 + 6 = 126$;
Ta có bảng sau:
| x | 0 | 1 | 2 | 3 |
| y | 6 | 46 | 86 | 126 |
Bảng này thể hiện khoảng cách của xe khách so với bưu điện Nha Trang sau 0 giờ; 1 giờ; 2 giờ; 3 giờ.
Khám phá 3 trang 18 Toán 8 Tập 2:
Hùng mua x mét dây điện và phải trả số tiền là y nghìn đồng. Giá trị tương ứng giữa x và y được cho bởi bảng sau:
| x | 1 | 2 | 3 | 4 |
| y | 4 | 8 | 12 | 16 |
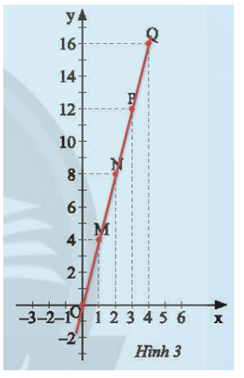
Hùng vẽ các điểm M(1; 4), N(2; 8), P(3; 12), Q(4; 16) trên mặt phẳng tọa độ Oxy như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm O, M, N, P, Q có thẳng hàng không.

Lời giải:
Dùng thước kiểm tra ta thấy O, M, N, P, Q thẳng hàng.
Giải Toán 8 trang 20 Tập 2
Thực hành 3 trang 20 Toán 8 Tập 2:
a) Vẽ đồ thị của các hàm số: y = 0,5x; y = −3x; y = x.
b) Các đồ thị sau đây là đồ thị của hàm số nào?
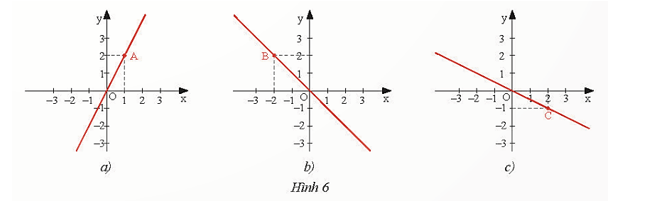
Lời giải:
a)
+) Đồ thị y = 0,5x
Cho x = 2 ta có y = 1. Ta vẽ điểm A (2; 1).
Đồ thị hàm số y = 0,5x là đường thẳng đi qua các điểm O(0; 0) và A(2; 1).

+) Đồ thị y = −3x
Cho x = 1 ta có y = −3. Ta vẽ điểm B (1; −3),
Đồ thị hàm số y = −3x là đường thẳng đi qua các điểm O(0; 0) và A(1; −3),

+) Đồ thị y = x
Cho x = 2 ta có y = 2. Ta vẽ điểm K (2; 2).
Đồ thị hàm số y = x là đường thẳng đi qua các điểm O(0; 0) và K(2; 2).

b)
+) Đồ thị Hình 6a) đi qua A(1; 2) và O(0; 0) suy ra đây là đồ thị hàm số y = 2x.
+) Đồ thị Hình 6b) đi qua B(−2; 2) và O(0; 0) suy ra đây là đồ thị của hàm số y = −x.
+) Đồ thị Hình 6c) đi qua C(2; −1) và O(0; 0) suy ra đây là đồ thị của hàm số
y = −0,5x.
Khám phá 4 trang 20 Toán 8 Tập 2:
Cho hai hàm số y = f(x) = x và y = g(x) = x + 3.
a) Thay dấu ? bằng số thích hợp
| x | −2 | −1 | 0 | 1 | 2 |
| y = f(x) = x | ? | ? | ? | ? | ? |
| y = g(x) = x + 3 | ? | ? | ? | ? | ? |
b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị hàm số y = f(x) và biều diễn các điểm có tọa độ thỏa mãn hàm số y = g(x) có trong bảng trên.
c) Kiểm tra xem các điểm thuộc đồ thị hàm số y = g(x) vẽ ở câu b có thẳng hàng không? Và dự đoán cách vẽ đồ thị của hàm số y = g(x).
Lời giải:
a)
| x | −2 | −1 | 0 | 1 | 2 |
| y = f(x) = x | −2 | −1 | 0 | 1 | 2 |
| y = g(x) = x + 3 | 1 | 2 | 3 | 4 | 5 |
b) Đồ thị hàm số y = f(x) đi qua điểm O(0; 0) và điểm có tọa độ A(1; 1).
Đồ thị hàm số y = f(x) đi qua điểm B(−2; 1), C(−1; 2), D(0; 3), E(1; 4), F(2; 5).

c) Các điểm thuộc đồ thị hàm số y = g(x) thẳng hàng với nhau nên đồ thị hàm số
y = g(x) song song với đồ thị hàm số y = f(x).
Giải Toán 8 trang 21 Tập 2
Thực hành 4 trang 21 Toán 8 Tập 2:
Vẽ đồ thị của các hàm số sau:
a) y = 5x + 2;
b) y = −2x – 6.
Lời giải:
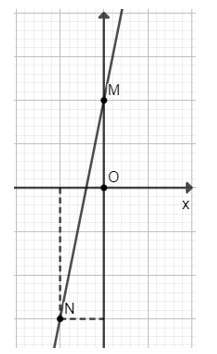
a) Với đồ thị hàm số y = 5x + 2
• Cho x = 0 thì y = 2.
• Cho x = −1 thì y = −3.
Đồ thị của hàm số y = 5x + 2 là đường thẳng đi qua hai điểm M(0; 2) và N(−1; −3).
b) Với đồ thị hàm số y = −2x – 6.
• Cho x = 0 thì y = −6.
• Cho y = 0 thì x = −3.
Đồ thị của hàm số y = −2x − 6là đường thẳng đi qua hai điểm P(0; −6) và Q(−3; 0).

Vận dụng 3 trang 21 Toán 8 Tập 2:
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết khi treo thêm lò xo một vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài y (cm) của lò xo theo khối lượng x (kg) của vật.
b) Vẽ đồ thị của hàm số y theo biến số x.

Lời giải:
a) y = 3x + 10 (cm)
b) Với đồ thị hàm số y = 3x +10.
• Cho x = −3 thì y = 1.
• Cho x = −2 thì y = 4.
Đồ thị hàm số y = 3x +10 là đường thẳng đi qua hai điểm A(−3; 1) và B(−2; 4).
Giải toán 8 tập 2 trang 22
Bài 1 trang 22 Toán 8 tập 2 CTST
Tìm các hàm số bậc nhất trong các hàm số sau đây và xác định các hệ số a, b của chúng
a) y = 4x + 2;
b) y = 5 – 3x;
c) y = 2 + x2;
d) y = −0,2x;
e. $y=\sqrt{5x}+1$
Gợi ý đáp án
a) y = 4x + 2 là hàm số bậc nhất với a = 4, b = 2.
b) y = 5 – 3x là hàm số bậc nhất với a = −3, b = 5
c) y= 2 + x2 không là hàm số bậc nhất.
d) y = −0,2x là hàm số bậc nhất với a = y = −0,2, b = 0.
e. $y=\sqrt{5x}+1$ là hàm số bậc nhất với a=$-\sqrt{5}$ b = −1.
bài 2 trang 22 Toán 8 Tập 2 CTST
Với giá trị nào của m thì mỗi hàm số sau đây là hàm số bậc nhất?
a) y = (m − 1)x + m;
b) y = 3 − 2mx.
Lời giải:
a) Điều kiện để hàm số y = (m − 1)x + m là hàm số bậc nhất là m − 1 ≠ 0 hay m ≠ 1.
b) Điều kiện để hàm số y = 3 − 2mx là hàm số bậc nhất là −2m ≠ 0 hay m ≠ 0.
Bài 3 trang 22 Toán 8 tập 2 CTST
a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
y = x; y = x + 2; y = −x; y = −x + 2 .
b) Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích.
Gợi ý đáp án
a) • Với hàm số y = x, cho x = 1 thì y = 1.
Đồ thị hàm số y = x đi qua các điểm O(0; 0) và C(1; 1).
• Với hàm số y = x + 2, cho x = 0 thì y = 2, cho x = −1 thì y = 1.
Đồ thị hàm số y = x + 2 đi qua các điểm B(0; 2) và A(−1; 1).
• Với hàm số y = −x, cho x = −1 thì y = 1.
Đồ thị hàm số y = −x đi qua các điểm O(0; 0) và A(−1; 1).
• Với hàm số y = −x + 2, cho x = 0 thì y = 2, cho x = 1 thì y = 1.
Đồ thị hàm số y = −x + 2 đi qua các điểm B (0; 2) và C(1; 1).
b) Ta có: Đường thẳng y = x song song với đường thẳng y = x + 2 suy ra OC // AB .
Đường thẳng y = −x song song với đường thẳng y = −x + 2 suy ra OA // BC .
Tứ giác OABC có: OC // AB, OA // BC
Suy ra tứ giác OABC là hình bình hành .
Hình bình hành OABC có hai đường chéo OB và AC vuông góc và bằng nhau nên tứ giác OABC là hình vuông.
Bài 5 trang 22 Toán 8 tập 2 CTST
Gọi C và r lần lượt là chu vi và bán kính của một đường tròn. Hãy chứng tỏ C là một hàm số bậc nhất theo biến số r. Tìm hệ số a, b của hàm số này.
Gợi ý đáp án
Công thức tính chu vi hình tròn là: C = 2πr
Hàm số C = 2πr có dạng y = ax + b với a = 2π ≠ 0 và b = 0 nên C là một hàm số bậc nhất theo biến số r.
Bài 6 trang 22 Toán 8 tập 2 CTST
Một người đi bộ trên đường thẳng với tốc độ v (km/h). Gọi s (km) là quãng đường đi được trong t (giờ).
a) Lập công thức tính s theo t.
b) Vẽ đồ thị của hàm số s theo biến số t khi v = 4.
Gợi ý đáp án
a) s = vt.
b) Hàm số: s = 4t.
Đồ thị hàm số s = 4t là đường thẳng đi qua 2 điểm O(0; 0); A(1; 4).
