Bài 3 Phép cộng và phép trừ đa thức một biến

Giải toán 7 tập 2 trang 36 bài 3 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải toán 7 tập 2 trang 33

Khởi động trang 33 Toán 7 tập 2 CTST

Có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực không?

Hướng dẫn giải:

Ta có thể cộng và trừ hai đa thức một biến như cộng và trừ hai số thực.

Khám phá 1 trang 33 Toán 7 tập 2 CTST

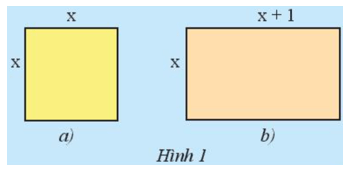
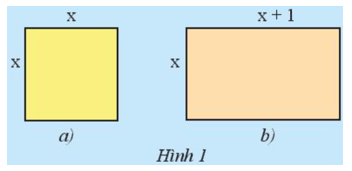
Hãy lập biểu thức biểu thị tổng chu vi của hình vuông (Hình 1a) và hình chữ nhật (Hình 1b).

Hướng dẫn giải:

Biểu thức biểu thị chu vi của hình vuông là: 4x.

Biểu thức biểu thị chu vi của hình chữ nhật là: 2 . (x + x + 1) = 2 . (2x + 1) = 2 . 2x + 2 . 1 = 4x + 2.

Biểu thức biểu thị tổng chu vi của hình vuông và hình chữ nhật là: 4x + 4x + 2 = 8x + 2.

Giải toán 7 tập 2 trang 34

Khám phá 2 trang 34 Toán 7 tập 2 CTST

Hình 2 gồm một hình chữ nhật có chiều dài 4x cm, chiều rộng 2x cm và hình vuông nhỏ bên trong có cạnh x cm.

Hãy lập biểu thức biểu thị diện tích của phần được tô màu vàng trong Hình 2.

Hướng dẫn giải:

Biểu thức biểu thị diện tích của hình chữ nhật là: 4x . 2x = 8x².

Biểu thức biểu thị diện tích của hình vuông là: x².

Biểu thức biểu thị diện tích phần được tô vàng trong Hình 2 là: 8x² – x² = 7x².

Giải toán 7 tập 2 trang 35

Thực hành 3 trang 35 Toán 7 tập 2 CTST

Thực hiện phép tính: (x – 4) + [(x² + 2x) + (7 – x)].

Hướng dẫn giải:

(x – 4) + [(x² + 2x) + (7 – x)]

= x – 4 + x² + 2x + 7 – x

= x² + (x + 2x – x) + (-4 + 7)

= x² + 2x + 3

Giải bài 1 trang 35 Toán 7 tập 2 CTST

Cho hai đa thức $P(x) = -3x^{4}-8x^{2}+2x$và $Q(x)=5x^{3}-3x^{2}+4x-6$. Hãy tính P(x) + Q(x) và P(x) – Q(x)

Gợi ý đáp án:

$P(x)+Q(x)=-3x^{4}-8x^{2}+2x+5x^{3}-3x^{2}+4x-6$

$= -3x^{4}+5x^{3}+(-8x^{2}-3x^{2})+2x+4x-6$

$=-3x^{4}+5x^{3}-11x^{2}+6x-6$

$P(x)-Q(x)=(-3x^{4}-8x^{2}+2x)-(5x^{3}-3x^{2}+4x-6)$

$= -3x^{4}-5x^{3}+(-8x^{2}+3x^{2})+2x-4x+6$

$=-3x^{4}-5x^{3}-5x^{2}-2x+6$

Giải bài 2 trang 35 Toán 7 tập 2 CTST

Cho đa thức $M(x) = 7x^{3}-2x^{2}+8x+4$. Tìm đa thức N(x) sao cho $M(x) + N(x) = 3x^{2}-2x$

Gợi ý đáp án:

$N(x)=(3x^{2}-2x)-M(x)=(3x^{2}-2x)-(7x^{3}-2x^{2}+8x+4)$

$=3x^{2}-2x-7x^{3}+2x^{2}-8x-4$

$=-7x^{3}+5x^{2}-10x-4$

Vậy $N(x) = -7x^{3}+5x^{2}-10x-4$.

Giải toán 7 tập 2 trang 36

Giải bài 3 trang 36 Toán 7 tập 2 CTST

Cho đa thức $A(y) = -5y^{4}-4y^{2}+2y+7$

Tìm đa thức B(y) sao cho $B(y) – A(y) = 2y^{3}-9y^{2}+4y$

Gợi ý đáp án:

$B(y)=A(y)+2y^{3}-9y^{2}+4y=-5y^{4}-4y^{2}+2y+7+2y^{3}-9y^{2}+4y$

$=-5y^{4}+2y^{3}-13y^{2}+6y+7$

Vậy $B(y) = -5y^{4}+2y^{3}-13y^{2}+6y+7$

Giải bài 4 trang 36 Toán 7 tập 2 CTST

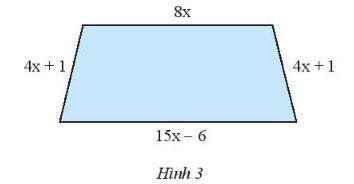
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3.

Gợi ý đáp án:

Chu vi hình thang là: 8x + (15x – 6) + 2(4x+1) = 31x – 4

Giải bài 5 trang 36 Toán 7 tập 2 CTST

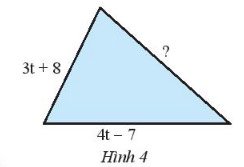
Cho tam giác (Hình 4) có chu vi bằng 12t – 3. Tìm cạnh chưa biết của tam giác đó.

Gợi ý đáp án:

Cạnh chưa biết của tam giác là: 12t – 3 – (3t + 8) – (4t – 7) = 5t – 4.

Giải bài 6 trang 36 Toán 7 tập 2 CTST

Cho ba đa thức $P(x) = 9x^{4}-3x^{3}+5x-1$

$Q(x) = -2x^{3}-5x^{2}+3x-8$

$R(x) = -2x^{4}+4x^{2}+2x-10$

Tính P(x) + Q(x) + R(x) và P(x) – Q(x) – R(x).

Gợi ý đáp án:

$P(x)+Q(x)+R(x)$

$=(9x^{4}-3x^{3}+5x-1)+(-2x^{3}-5x^{2}+3x-8)+(-2x^{4}+4x^{2}+2x-10)$

$(9x^{4}-2x^{4})+(-3x^{3}-2x^{3})+(-5x^{2}+4x^{2})+(5x+3x+2x)+(-1-8-10)$

$=7x^{4}-5x^{3}-x^{2}+10x-19$

$P(x)-Q(x)-R(x)$

$=(9x^{4}-3x^{3}+5x-1)-(-2x^{3}-5x^{2}+3x-8)-(-2x^{4}+4x^{2}+2x-10)$

$=(9x^{4}+2x^{4})+(-3x^{3}+2x^{3})+(5x^{2}-4x^{2})+(5x-3x-2x)+(-1+8+10)$

$=11x^{4}-x^{3}+x^{2}+17$

Giải bài 7 trang 36 Toán 7 tập 2 CTST

Cho đa thức $P(x) = x^{3} – 4x^{2} + 8x -2$. Hãy viết P(x) thành tổng của hai đa thức bậc bốn.

Gợi ý đáp án:

$P(x) = x^{3} – 4x^{2} + 8x -2$

$= (x^{4} – x^{3} – 2x^{2} + 8x – 5) + (-x^{4} + 2x^{3} – 2x^{2} + 3)$

Giải bài 8 trang 36 Toán 7 tập 2 CTST

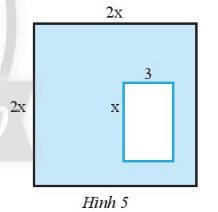
Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (hình 5). Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.

Gợi ý đáp án:

Diện tích hình vuông là: $2x.2x = 4x^{2}$.

Diện tích hình chữ nhật là: 3.x

Diện tích phần được tô xanh là: $4x^{2} – 3x$

Giải bài 9 trang 36 Toán 7 CTST

a. Thực hiện phép tính: $(3x-1)+[(2x^{2}+5x)+(4-3x)]$

b. Cho A= 4x+2, $C=5-3x^{2}$. Tìm đa thức B sao cho A+B=C

Gợi ý đáp án:

a) $(3x-1)+[(2x^{2}+5x)+(4-3x)]$

$= (3x-1)+[(2x^{2}+5x)+(4-3x)]=(3x-1)+(2x^{2}+2x+4)$

$=3x-1+2x^{2}+2x+4$

$=2x^{2}+5x+3$

b) $B = C – A = 5-3x^{2} – 4x – 2 = -3x^{2}-4x+3$