Giải toán 11 tập 2 trang 86 bài tập cuối chương 8

Giải toán 11 tập 2 trang 86 Bài tập cuối chương 8 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải toán 11 tập 2 trang 86

Giải bài 1 trang 86 Toán 11 tập 2

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây?

A. (SAD)

B. (SAC)

C. (SAB)

D. (SBD)

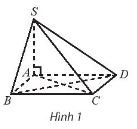
Bài làm

Vì SA ⊥ (ABCD) nên SA ⊥ CD

Mà CD ⊥ AD nên CD ⊥ (SAD)

Đáp án: A

Giải bài 2 trang 86 Toán 11 tập 2

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC = $2b\sqrt{2}$. Số đo góc giữa cạnh bên SC và mặt đáy là:

A. 60^o

B. 30^o

C. 45^o

D. 50^o

Bài làm

Đáp án A

Giải bài 3 trang 86 Toán 11 tập 2

Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

A. (SBC)

B. (SAC)

C. (SBD)

D. (ABCD)

Bài làm

Đáp án B

Giải bài 4 trang 86 Toán 11 tập 2

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và chiều cao bằng $a\sqrt{2}$. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là:

A.$\frac{a\sqrt{14}}{7}$

B. $\frac{a\sqrt{2}}{7}$

C. $\frac{a\sqrt{14}}{2}$

D. $\frac{2a\sqrt{14}}{7}$

Bài làm

Đáp án A

Giải bài 5 trang 86 Toán 11 CTST

Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng $\frac{a\sqrt{6}}{3}$ là:

A. $\frac{7\sqrt{2}}{8}a^{3}$

B. $\frac{\sqrt{2}}{4}a^{3}$

C. $\frac{7\sqrt{2}}{12}a^{3}$

D. $\frac{7\sqrt{3}}{4}a^{3}$

Bài làm

Đáp án C

Giải bài 6 trang 86 Toán 11 tập 2

Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S,BC,A] có số đo là:

A. 75^o46′

B. 71^o21′

C. 68^o31′

D. 65^o12′

Bài làm

Đáp án D

Giải bài 7 trang 86 Toán 11 tập 2

Nếu hình hộp chữ nhật có ba kích thước là 3;4;5 thì độ dài đường chéo của nó là:

A. $5\sqrt{2}$

B. 50

C. $2\sqrt{5}$

D. 12

Bài làm

Đáp án A

Giải bài 8 trang 86 Toán 11 tập 2

Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là:

A. $\frac{a^{3}.\sqrt{3}}{4}$

B. $\frac{a^{3}.\sqrt{3}}{3}$

C. $\frac{a^{3}.\sqrt{2}}{3}$

D. $\frac{a^{3}.\sqrt{2}}{2}$

Bài làm

Diện tích đáy của khối lăng trụ là: $S = \frac{{{a^2}\sqrt 3 }}{4}$

Chiều cao của khối lăng trụ là cạnh bên của lăng trụ bằng: $h = a$

Thể tích của khối lăng trụ là: $V = Sh = \frac{{{a^3}\sqrt 3 }}{4}$

Đáp án A

Giải bài 9 trang 86 Toán 11 CTST

Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M, N lần lượt là trung điểm của AB và AD.

a) Chứng minh rằng (SMD) ⊥ (SNC)

b) Tính khoảng cách từ M đến mặt phẳng (SNC)

Bài làm

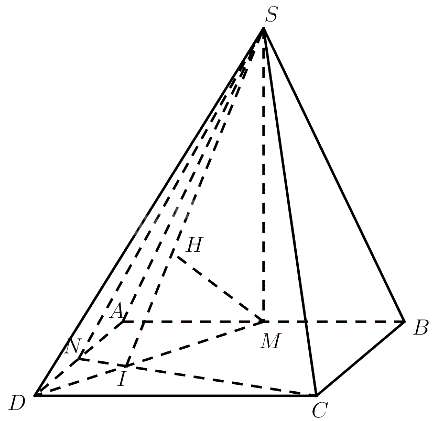
Gọi $I = CN \cap DM$

$\Delta SAB$ đều $ \Rightarrow SM \bot AB$

Mà $\left( {SAB} \right) \bot \left( {ABCD} \right),\left( {SAB} \right) \cap \left( {ABCD} \right) = AB$

$ \Rightarrow SM \bot \left( {ABCD} \right) \Rightarrow SM \bot CN$

$\Delta A{\rm{D}}M = \Delta DCN\left( {c.g.c} \right) \Rightarrow \widehat {AM{\rm{D}}} = \widehat {CN{\rm{D}}}$

Mà $\widehat {AM{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ }$

$\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ } \Rightarrow \widehat {NI{\rm{D}}} = {180^ \circ } – \left( {\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M}} \right) = {90^ \circ } \Rightarrow CN \bot DM$

$\left. \begin{array}{l}\left. \begin{array}{l}SM \bot CN\\CN \bot DM\end{array} \right\} \Rightarrow CN \bot \left( {SM{\rm{D}}} \right)\\CN \subset \left( {SNC} \right)\end{array} \right\} \Rightarrow \left( {SNC} \right) \bot \left( {SM{\rm{D}}} \right)$

b) Kẻ $MH \bot SI\left( {H \in SI} \right)$

$CN \bot \left( {SM{\rm{D}}} \right) \Rightarrow CN \bot MH$

$ \Rightarrow MH \bot \left( {SNC} \right) \Rightarrow d\left( {M,\left( {SNC} \right)} \right) = MH$

$\Delta C{\rm{D}}N$ vuông tại $D$ có đường cao $DI$

$DN = \frac{1}{2}A{\rm{D}} = \frac{a}{2},CN = \sqrt {C{{\rm{D}}^2} + D{N^2}}  = \frac{{a\sqrt 5 }}{2},DI = \frac{{C{\rm{D}}.DN}}{{CN}} = \frac{{a\sqrt 5 }}{5}$

$DM = CN = \frac{{a\sqrt 5 }}{2} \Rightarrow MI = DM – DI = \frac{{3a\sqrt 5 }}{{10}}$

$\Delta SAB$ đều $ \Rightarrow SM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}$

$\Delta SMI$ vuông tại $M$ có đường cao $MH$

$ \Rightarrow MH = \frac{{SM.MI}}{{\sqrt {S{M^2} + M{I^2}} }} = \frac{{3a\sqrt 2 }}{8}$

Vậy $d\left( {M,\left( {SNC} \right)} \right) = \frac{{3a\sqrt 2 }}{8}$

Giải toán 11 tập 2 trang 87

Giải bài 10 trang 87 Toán 11 CTST

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (SABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP

Bài làm

Lời giải

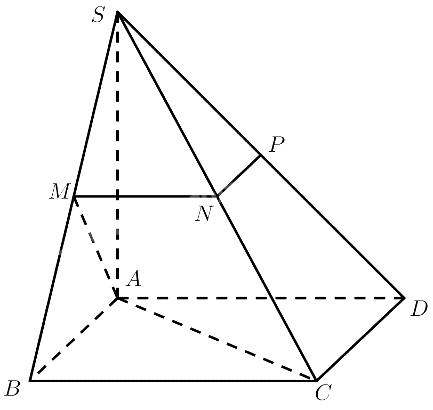
$M$ là trung điểm của $SB$

$N$ là trung điểm của $SC$

$ \Rightarrow MN$ là đường trung bình của $\Delta SBC$

$\left. \begin{array}{l} \Rightarrow MN\parallel BC\\BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow MN \bot C{\rm{D}}$

Mà $C{\rm{D}}\parallel NP$ $ \Rightarrow MN \bot NP$ (1)

$\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)$

Mà $MN\parallel BC$$ \Rightarrow MN \bot \left( {SAB} \right) \Rightarrow MN \bot AM$(2)

Từ (1) và (2) $ \Rightarrow d\left( {AM,NP} \right) = MN = \frac{1}{2}BC = \frac{a}{2}$.

Giải bài 11 trang 87 Toán 11 tập 2

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60^o. Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.

Lời giải

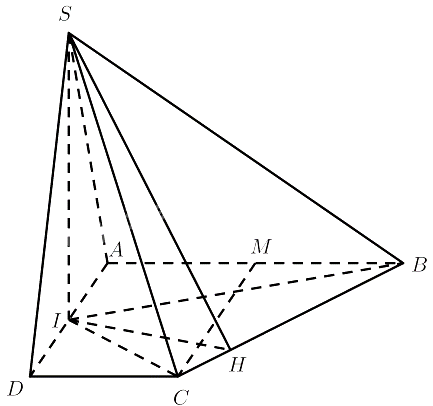
$\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)$

Kẻ $IH \bot BC\left( {H \in BC} \right)$

$SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC$

$ \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH$

Vậy $\widehat {AHI}$ là góc nhị diện $\left[ {S,BC,A} \right]$$ \Rightarrow \widehat {AHI} = {60^ \circ }$

$\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} – {S_{AIB}} – {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}$

Gọi $M$ là trung điểm của $AB$

$\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}}  = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}$

${V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}$

Giải bài 12 trang 87 Toán 11 CTST

Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh dáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng bên trong bằng $\frac{a}{2}$

a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy

b) Tính thể tích chân cột nói trên theo a

Lời giải

Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều $ABCD.A’B’C’D’$ với $O,O’$ là tâm của hai đáy. Vậy $AB = 2{\rm{a}},A’B’ = a,OO’ = 2a$.

Gọi $M,M’$ lần lượt là trung điểm của $CD,C’D’$.

$A’B’C'{\rm{D}}’$ là hình vuông $ \Rightarrow O’M’ \bot C'{\rm{D}}’$

$CDD’C’$ là hình thang cân $ \Rightarrow MM’ \bot C’D’$

Vậy $\widehat {MM’O’}$ là góc phẳng nhị diện giữa mặt bên và đáy nhỏ, $\widehat {M’MO}$ là góc phẳng nhị diện giữa mặt bên và đáy lớn.

Kẻ $M’H \bot OM\left( {H \in OM} \right)$

$OMM’O’$ là hình chữ nhật

$ \Rightarrow OH = O’M’ = \frac{a}{2},OM = a,MH = OM – OH = \frac{{\rm{a}}}{2}$

$\begin{array}{l}\tan \widehat {M’MO} = \frac{{M’H}}{{MH}} = 4\\ \Rightarrow \widehat {M’MO} = 75,{96^ \circ } \Rightarrow \widehat {MM’O’} = {180^ \circ } – \widehat {M’MO} = 104,{04^ \circ }\end{array}$

b) Diện tích đáy lớn là: $S = A{B^2} = 4{{\rm{a}}^2}$

Diện tích đáy bé là: $S’ = A’B{‘^2} = {a^2}$

Thể tích hình chóp cụt là: ${V_1} = \frac{1}{3}h\left( {S + \sqrt {SS’}  + S’} \right) = \frac{1}{3}.2a\left( {4{{\rm{a}}^2} + \sqrt {4{{\rm{a}}^2}.{a^2}}  + {a^2}} \right) = \frac{{14{{\rm{a}}^3}}}{3}$

Thể tích hình trụ rỗng là: ${V_2} = \pi {R^2}h = \pi .{\left( {\frac{a}{2}} \right)^2}.2{\rm{a}} = \frac{{\pi {a^3}}}{2}$

Thể tích chân cột là: $V = {V_1} – {V_2} = \left( {\frac{{14}}{3} – \frac{\pi }{2}} \right){a^3}$.

Giải bài 13 trang 87 Toán 11 tập 2

Cho hình hộp ABCD.A’B’C’D’ có cạnh bên AA’ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A’ lên mặt đáy trùng với điểm O là giao điểm hai đường chéo của đáy. Tính thể tích của khối chóp.

Lời giải

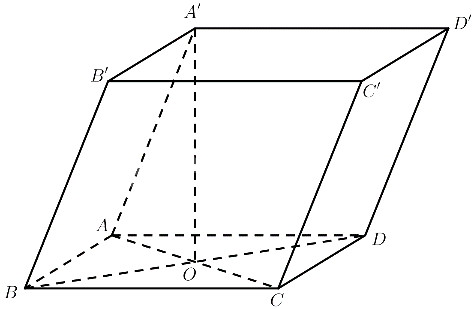
$AB = B{\rm{D}} = A{\rm{D}} = a \Rightarrow \Delta ABD$ đều$ \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ }$

$O$ là trung điểm của $BD$$ \Rightarrow AO = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}$

$\begin{array}{l}AA’ \bot \left( {ABCD} \right) \Rightarrow AA’ \bot AO\\ \Rightarrow A’O = \sqrt {AA{‘^2} – A{O^2}}  = \frac{a}{2}\end{array}$

${S_{ABC{\rm{D}}}} = AB.A{\rm{D}}.\sin \widehat {BA{\rm{D}}} = \frac{{{a^2}\sqrt 3 }}{2}$

${V_{ABCD.A’B’C’D’}} = {S_{ABC{\rm{D}}}}.A’O = \frac{{{a^3}\sqrt 3 }}{4}$