Toán 11 tập 2 trang 106 Bài 5: Khoảng cách

Giải toán 11 tập 2 trang 106 Bài 5 sách Cánh diều có đáp án chi tiết từng bài tập trong sách giáo khoa Toán lớp 11 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Trang 101 toán 11 tập 2

Hoạt động 1 trang 101 toán 11 tập 2

Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí $M$ trên tường có độ cao so với nền nhà là $MH = 80cm$. Quan sát Hình 61, nền nhà gợi nên mặt phẳng $\left( P \right)$, cho biết độ dài đoạn thẳng $MH$ gợi nên khái niệm gì trong hình học liên quan đến điểm $M$ và mặt phẳng $\left( P \right)$.

Lời giải:

Độ dài đoạn thẳng $MH$ gợi nên khái niệm khoảng cách từ một điểm đến một mặt phẳng.

Luyện tập 1 trang 101 toán 11 tập 2

Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right),AI \bot BC\left( {I \in BC} \right)$, $AH \bot SI\left( {H \in SI} \right)$. Chứng minh rằng khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng $AH$.

Lời giải:

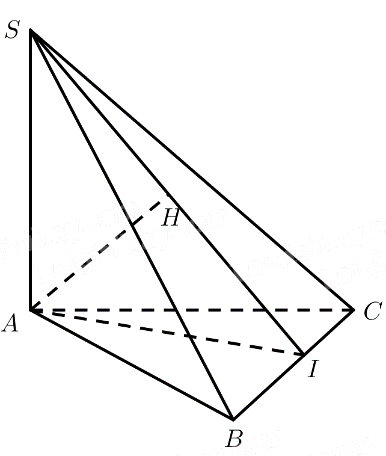
Ta có:

$\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAI} \right)\\\left. \begin{array}{l} \Rightarrow BC \bot AH\\AH \bot SI\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right)\end{array}$

Vậy $d\left( {A,\left( {SBC} \right)} \right) = AH$.

Trang 102 toán 11 tập 2

Hoạt động 2 trang 102 toán 11 tập 2

Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song $\Delta $ và $\Delta ‘$. Xét điểm $A$ trên đường thẳng $\Delta $.

a) Khoảng cách từ điểm $A$ đến đường thẳng $\Delta ‘$ có phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta $ hay không? Vì sao?

b) Khoảng cách đó gợi nên khái niệm gì trong hình học liên quan đến hai đường thẳng song song $\Delta $ và $\Delta ‘$?

Lời giải:

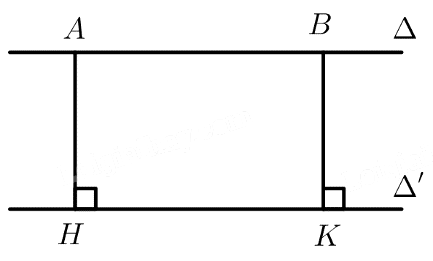
a) Trên đường thẳng $\Delta $ lấy điểm $B$ khác $A$.

Kẻ $AH \bot \Delta ‘,BK \bot \Delta ‘\left( {H,K \in \Delta ‘} \right)$

$ABKH$ là hình chữ nhật $ \Rightarrow AH = BK$

$ \Rightarrow d\left( {A,\Delta ‘} \right) = d\left( {B,\Delta ‘} \right)$

Vậy khoảng cách từ điểm $A$ đến đường thẳng $\Delta ‘$ không phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta $.

b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai đường thẳng song song.

Luyện tập 2 trang 102 toán 11 tập 2

Người ta dựng các cột đèn vuông góc với mặt đường, trong đó mỗi cột đèn gợi nên hình ảnh một đường thẳng. Khoảng cách giữa hai chân cột đèn liên tiếp đo được là 5 m. Tại sao có thể nói khoảng cách giữa hai cột đèn đó là 5 m.

Lời giải:

Các cột đèn được dựng thẳng đứng và vuông góc với mặt đường thì chúng song song với nhau. Do đó, đoạn thẳng nối hai chân cột chính là khoảng cách giữa hai đường thẳng song song. Vậy ta có thể nói khoảng cách giữa hai cột đèn đó là 5 m.

Hoạt động 3 trang 102 toán 11 tập 2

Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ song song với nhau, chiều cao của chiếc cột có đỉnh cột $A$ là khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$.

a) Khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$ có phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta $ hay không? Vì sao?

b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$?

Lời giải:

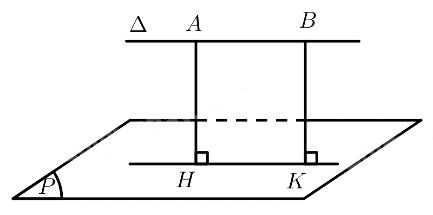
a) Trên đường thẳng $\Delta $ lấy điểm $B$ khác $A$.

Kẻ $AH \bot \left( P \right),BK \bot \left( P \right)\left( {H,K \in \left( P \right)} \right)$

$ \Rightarrow ABKH$ là hình chữ nhật $ \Rightarrow AH = BK$

$ \Rightarrow d\left( {A,\left( P \right)} \right) = d\left( {B,\left( P \right)} \right)$

Vậy khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$ không phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta $.

b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa đường thẳng và mặt phẳng song song.

Trang 103 toán 11 tập 2

Luyện tập 3 trang 103 toán 11 tập 2

Cho hình chóp $S.ABC$ có $SA = a$, góc giữa $SA$ và $mp\left( {ABC} \right)$ là ${60^ \circ }$. Gọi $M,N$ lần lượt là trung điểm của cạnh $SA$ và $SB$. Chứng minh $MN\parallel \left( {ABC} \right)$ và tính $d\left( {MN,\left( {ABC} \right)} \right)$.

Lời giải:

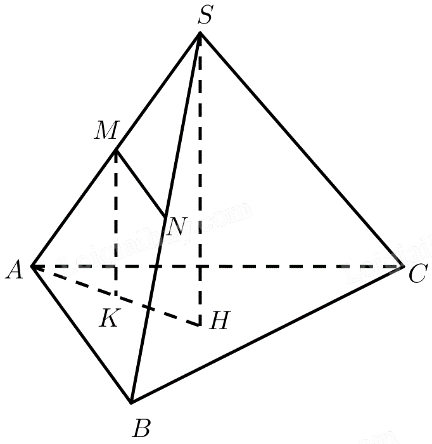
Ta có: $M$ là trung điểm của $SA$

$N$ là trung điểm của $SB$

$ \Rightarrow MN$ là đường trung bình của $\Delta SAB$

$\left. \begin{array}{l} \Rightarrow MN\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABC} \right)$

$ \Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right)$

Gọi $H$ là hình chiếu vuông góc của $S$ lên $\left( {ABC} \right)$$ \Rightarrow SH \bot \left( {ABC} \right)$

Qua $M$ kẻ đường thẳng song song với $SH$, cắt $\left( {ABC} \right)$ tại $K$

$ \Rightarrow K \in AH,MK \bot \left( {ABC} \right) \Rightarrow d\left( {M,\left( {ABC} \right)} \right) = MK$

$\begin{array}{l}SH \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,HA} \right) = \widehat {SAH} = {60^ \circ }\\ \Rightarrow SH = SA.\sin \widehat {SAH} = \frac{{a\sqrt 3 }}{2}\end{array}$

$M$ là trung điểm của $SA$, $MK\parallel SH$

$ \Rightarrow MK$ là đường trung bình của $\Delta SAH$

$ \Rightarrow MK = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}$

Vậy $d\left( {MN,\left( {ABC} \right)} \right) = \frac{{a\sqrt 3 }}{4}$

Hoạt động 4 trang 103 toán 11 tập 2

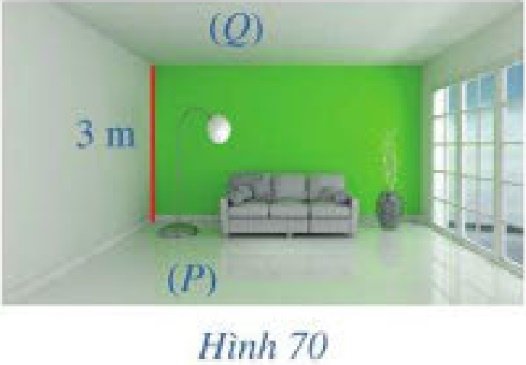
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song $\left( P \right),\left( Q \right)$. Chiều cao của căn phòng là 3 m.

Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song $\left( P \right),\left( Q \right)$?

b) Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ song song với nhau. Xét điểm $I$ tuỳ ý trong mặt phẳng $\left( P \right)$, lấy $K$ là hình chiếu của $I$ trên $\left( Q \right)$ (Hình 71). Khoảng cách $IK$ từ điểm $I$ đến mặt phẳng $\left( Q \right)$ có phụ thuộc vào vị trí của điểm $I$ trong mặt phẳng $\left( P \right)$ hay không? Vì sao?

Lời giải:

a) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song.

b)

Trên mặt phẳng $\left( P \right)$ lấy điểm $J$ khác $I$.

Kẻ $JH \bot \left( Q \right)\left( {H \in \left( Q \right)} \right)$

$ \Rightarrow HKIJ$ là hình chữ nhật $ \Rightarrow IK = JH$

$ \Rightarrow d\left( {I,\left( Q \right)} \right) = d\left( {J,\left( Q \right)} \right)$

Vậy khoảng cách $IK$ từ điểm $I$ đến mặt phẳng $\left( Q \right)$ không phụ thuộc vào vị trí của điểm $I$ trong mặt phẳng $\left( P \right)$.

Trang 104 toán 11 tập 2

Luyện tập 4 trang 104 toán 11 tập 2

Cho hình lăng trụ $ABC.A’B’C’$ có cạnh bên bằng $a$, góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^ \circ }$. Tính khoảng cách giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {A’B’C’} \right)$.

Lời giải:

Gọi $H$ là hình chiếu vuông góc của $A’$ lên $\left( {ABC} \right)$

$\begin{array}{l} \Rightarrow A’H \bot \left( {ABC} \right)\\ \Rightarrow \left( {AA’,\left( {ABC} \right)} \right) = \left( {AA’,AH} \right) = \widehat {A’AH}\end{array}$

$\Delta AA’H$ vuông tại $H \Rightarrow A’H = AA’.\sin \widehat {A’AH} = \frac{{a\sqrt 3 }}{2}$

Vì $\left( {ABC} \right)\parallel \left( {A’B’C’} \right)$ nên $d\left( {\left( {ABC} \right),\left( {A’B’C’} \right)} \right) = d\left( {A’,\left( {ABC} \right)} \right) = A’H = \frac{{a\sqrt 3 }}{2}$

Hoạt động 5

Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng $a$ và $b$ chéo nhau, hai bản lề của cánh cửa nằm trên đường thẳng $c$.

Quan sát Hình 73 và cho biết đường thẳng $c$ có vừa cắt, vừa vuông góc với cả hai đường thẳng $a$ và $b$ hay không.

Lời giải:

Đường thẳng $c$ có vừa cắt, vừa vuông góc với cả hai đường thẳng $a$ và $b$.

Luyện tập 5

Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$. Tính $d\left( {SA,BC} \right)$.

Lời giải:

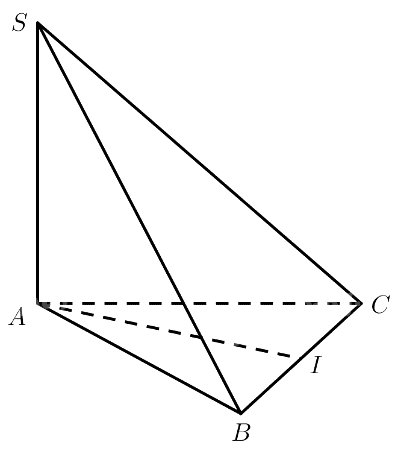
Gọi $I$ là trung điểm của $BC$.

Tam giác $ABC$ đều $ \Rightarrow AI \bot BC$

$SA \bot \left( {ABC} \right) \Rightarrow SA \bot AI$

$ \Rightarrow d\left( {SA,BC} \right) = AI = \frac{{BC\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}$

Trang 106 toán 11 tập 2

Bài 1 trang 106 SGK Toán 11 tập 2

Hình 76 gợi nên hình ảnh hai mặt phẳng (P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa (P) và (Q) là bao nhiêu mét?

Bài làm

Khoảng cách giữa (P) và (Q) là cây cột gỗ gao 4,2m

Bài 2 trang 106 SGK Toán 11 tập 2

Cho hình tứ diện ABCD có AB = a, BC = b, $\widehat{ABC}$ = $\widehat{ABD}$ = $\widehat{BCD}$ = 90^∘. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD

a) Tính khoảng cách từ điểm C đến đường thẳng AB.

b) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).

c) Tính khoảng cách giữa hai đường thẳng AB và CD.

Bài làm

a) Có $\widehat{ABC}$ = 90^∘

=> AB ⊥ BC => d(C,AB) = BC = b

b) Có $AB\perp BC, AB\perp BD$

=> AB ⊥ (BCD)

=> AB ⊥ CD

mà BC ⊥ CD (Vì $\widehat{BCD}$ = 90^∘)

=> CD ⊥ (ABC)

=> d(D,(ABC)) = CD = $\sqrt{BD^{2} – BC^{2} } = \sqrt{c^{2}-b^{2} }$

c) AB ⊥ BC, BC ⊥ CD => d(AB,CD) = BC = b

Bài 3 trang 106 SGK Toán 11 tập 2

Với giả thiết ở Bài tập 2, hãy:

a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC.

b) Chứng minh rằng MP // (BCD). Tính khoảng cách từ đường thẳng MP đến mặt phẳng (BCD).

c) Chứng minh rằng (MNP) || (BCD). Tính khoảng cách giữa hai mặt phẳng (MNP) và (BCD).

Bài làm

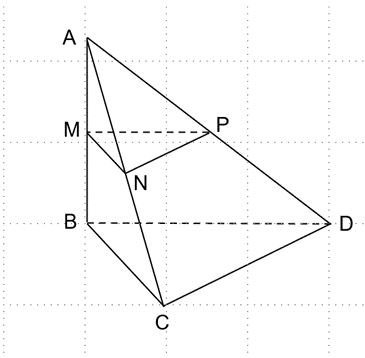
a) Có M là trung điểm của AB, N là trung điểm của AC

=> MN là đường trung bình của tam giác ABC

=> MN // BC

– Có AB ⊥ BC => MB ⊥ BC => d(MN,BC) = MB = $\frac{1}{2}$AB = $\frac{a}{2}$

b) Có M là trung điểm của AB, P là trung điểm của AD

=> MP là đường trung bình của tam giác ABD

=> MP // BD

mà BD ⊂ (BCD)

=> MP // (BCD)

Có AB ⊥ (BCD) => MB ⊥ (BCD)

=> d(MP,(BCD)) = d(M,(BCD)) = MB = $\frac{a}{2}$

c) Có MN // BC, BC ⊂ (BCD)

=> MN // (BCD)

mà MP // (BCD)

=> (MNP) // (BCD)

=> d((MNP), (BCD)) = d(M,(BCD)) = MB = $\frac{a}{2}$

Bài 4 trang 106 SGK Toán 11 tập 2

Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).

a) Tính khoảng cách từ điểm S đến đường thẳng CD.

b) Tính khoảng cách từ điểm D đến mặt phẳng (SAB).

c) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).

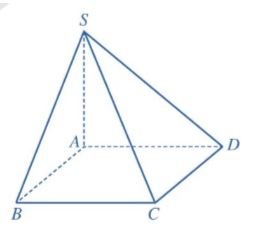
Bài làm

a) Có $SA\perp (ABCD) => SA\perp CD$

Có ABCD là hình vuông => $AD \perp CD$

=> $CD \perp (SAD) => CD\perp SD$

=> $d(S,CD)=SD=\sqrt{SA^{2}+AD^{2}}=a\sqrt{2}$

b) $SA\perp (ABCD)=>SA\perp AD$

ABCD là hình vuông => $AB\perp AD$

=> $AD\perp (SAB)=>d(D,(SAB))=AD=a$

c) Kẻ $AH\perp SD$

$CD\perp (SAD) => CD\perp AH$

=> $AH\perp (SCD)=>d(A,(SCD))=AH$

Tam giác SAD vuông tại A có đường cao AH

=> $AH=\frac{SA.AD}{SD}=\frac{a\sqrt{2}}{2}$

Bài 5 trang 106 SGK Toán 11 tập 2

Với giả thiết ở Bài tập 4, hãy:

a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).

b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.

Bài làm

a) ABCD là hình vuông => BC // AD

mà $AD \subset (SAD)$

=> $BC // (SAD) => d(BC,(SAD))=d(B, (SAD))$

$SA\perp (ABCD) => SA\perp AB$

ABCD là hình vuông

=> $AB\perp AD => AB\perp (SAD) => d(B, (SAD))=AB=a$

b) ABCD là hình vuông => $BD \perp AC$

$SA\perp (ABCD) => SA\perp BD$

=> $BD \perp (SAC)$

Gọi $O=AC\cap BD$, kẻ $OH\perp SC$

Có $BD \perp (SAC) => BD \perp OH$

=> d(BD, SC) = OH

Có tam giác ABC vuông tại B

=> $AC=a\sqrt{2}$

=> $OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$

Có $SA\perp (ABCD) => SA\perp AC$

=> Tam giác SAC vuông tại A

=> $SC=a\sqrt{3}$

Có $\Delta SAC\sim \Delta OHC (g.g)$

=> $\frac{SA}{OH}=\frac{SC}{OC}$

=> $OH=\frac{SA.OC}{SC}=\frac{a\sqrt{6}}{6}$